LEYES DE LA ELECTRODINAMICA

LEY DE OHM:

“En una corriente eléctrica, la diferencia de potencial
es directamente proporcional a la intensidad
de corriente eléctrica”

Si se representa la resistencia del conductor por la letra R, la diferencia de potencial en los extremos del conductor por la letra V, y la corriente que circula por él, con la letra I la ley de Ohm puede formularse como :

V= I x R

que es lo mismo que decir:

I = V / R ó R = V / I


La unidad de resistencia eléctrica es el OHMIO, simbolizado por la letra griega W (omega)
Los múltiplos más usuales del Ohmio son: El Kilohmio que es igual a 1.000 Ohmios => 1KW = 1.000 W El Megaohmio ques es igual a 1.000.000 Ohmios => 1MW = 1.000.000 W

La ley de Ohm relaciona el valor de la resistencia de un conductor con la intensidad de corriente que lo atraviesa y con la diferencia de potencial entre sus extremos. En el gráfico vemos un circuito con una resistencia y una pila. Observamos un amperímetro que nos medirá la intensidad de corriente, I. El voltaje que proporciona la pila V, expresado en voltios, esta intensidad de corriente, medido en amperios, y el valor de la resistencia en ohmios, se relacionan por la ley de Ohm, que aparece en el centro del circuito.

Dicha proporcionalidad se expresa como:

R = r x l / S

Donde: R es la resistencia medida en ohmios l es la longitud medida en metros. S es la sección (área) transversal del conductor, en metros cuadrados. r es una constante que depende del material con que está fabricado el conductor y se llama RESISTIVIDAD o RESISTENCIA ESPECIFICA del material en cuestión, y que da la resistencia por cada unidad de longitud y de sección.

COMENTARIO: yo creo que esta ley es importante ya que mediante sus formulas podemos hallar el voltaje , la intensidad de corriente , y la resistencia.
Nos ayuda a saber cuanto de voltaje por ejemplo entra o llega a nuestras casas y con cuanto de intensidad es decir nos dice el votaje que existe entre dos puntos de un conductor y la intensidad de corriente que pasa por 'el son directamente proporcionales.

LEYES DE KIRCHHOFF

La primera ley de Kirchhoff : ley de los nudos

la intensidad de coriente neta que llega a un nudo esigual a ala intensidad de corriente neta que sale de el.

En un nudo, la suma de las corrientes que entran es igual a las de que salen. O vien, la suma algebraica de corrientes en un nudo es nula.
Esto es evidente, ya que los electrones no se pueden acumular en un nudo, ni tampoco pueden producirse allí.

Ejemplo:

E= El + E2 + E3
E= 37,9 + 151,5 + 60,6
E= 250 V

La tensión que aparece a través de cada resistencia (la caída de tensión) puede obtenerse de la ley de Ohm.
Ejemplo: Si la tensión a través de Rl la llamamos El, a través de R2, E2, y a través de R3, E3, entonces:

El = IxRI = 0,00758 X 5000 = 37,9 V
E2 = IxR2 = 0,00758 X 20.000 = 151,5 V
E3 = IxR3 = 0,00758 X 8000 = 60,6 V

a) Asociación en paralelo

I= I1 + I2 + I3

En este montaje hay varias mallas , apareciendo, por lo tanto, NUDOS. La tensión en extremos de todas las resistencias es la MISMA. Lo que cambia es la corriente a través de cada una de ellas. La suma de todas las corrientes será igual a la corriente total suministrada por el generador (1ª Ley de Kirchoff)


Segunda ley de Kirchhoff: ley de los mayas

A lo largo de una malla, la suma de fuerzas electromotrices es igual a la suma de las diferencias de potencial producidas en las resistencias. Otra manera de expresar esto es: la suma algebraica de las tensiones a lo largo de una malla es cero. Obsérvese que esta ley no es sino la ley de Ohm generalizada

Esta ley viene a contemplar el reparto de tensiones en un circuito, descomponiéndolo en las diferentes caídas parciales.Al estudiar las caídas de tensión en un circuito serie se comprobó que la suma de las tensiones en bornes de cada elemento de consumo debía ser igual a la proporcionada por el generador.

V = Vl + V2 + V3

Cada una de las tensiones :

V1, V2 Y V3

es el resultado de multiplicar la intensidad general por cada una de las resistencias.La segunda ley de Kirchhoff generaliza estas explicaciones para aquellos circuitos serie o en las mallas de un circuito paralelo o en derivación en el que pueden existir uno o más generadores y diferentes elementos de consumo.

Todo circuito puede reducirse a un circuito elemental con un solo generador y un elemento de consumo, de manera que el comportamiento de ambos sea igual al comportamiento de todo el circuito completo.

Recordemos la asociación de resistencias en serie y paralelo:

b) Asociación en serie :

E = VI + VII + VIII

En este montaje tenemos UNA sola malla. No hay, por lo tanto, nudos. La corriente I que circula por la única malla es la MISMA para todas las resistencias. Lo que cambia es la tensión en cada una de ellas. La suma de todas las tensiones será igual a la f.e.m. E producida por el generador (2ª Ley de Kirchoff)

COMENTARIO: la primera y la segunda ley de kirchhoff son tan importante como la de ohm y a de joule pero en este caso popdemos decir que las dos leyes de kirchhoff nos son utiles para poder determinar la intensidad dse corriente de un circuito en una determinada resistencia claro esta que es con la ayuda de sus formulas.

LEY DE JOULE

La relación entre la cantidad de calor producido y el trabajo realizado es una constante llamada equivalente mecánico del calor.

Para deducir la cantidad de calor desarrollada en un conductor por unidad de tiempo, hallaremos primero la expresión general de la potencia suministrada a una parte cualquiera de un circuito eléctrico.

Cuando una corriente eléctrica atraviesa un conductor, éste experimenta un aumento de temperatura. Este efecto se denomina “efecto Joule”.

sabiendo que la energia disipada (E) por una resistencia esta relacionada con el voltaje (V) , la intensidad de corriente.

E=V.I.t

La ley de Joule enuncia que :

" El calor que desarrolla una corriente eléctrica al pasar por un conductor es directamente proporcional a la resistencia, al cuadrado de la intensidad de la corriente y el tiempo que dura la corriente " .

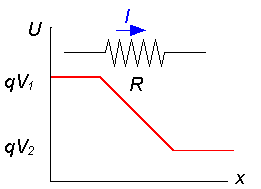
la rapidez con la que las cargas pierden la energía es la potencia disipada en la resistencia:


este resultado se conoce como Ley de Joule y expresa la pérdida de energía que las cargas experimentan en las colisiones atómicas que se producen en la resistencia.

La energía se disipa en forma de calor (efecto Joule).

COMENTARIO: a mi parecer esta ley es muy importante ya que con esta ley es posible calcular la cantidad de calor que puede producir una corriente electrica en un cierto tiempo.